OpenGL에서 모든 것은 3D 공간 안에 있습니다. 하지만 화면과 윈도우 창은 2차원 픽셀 배열입니다. 그렇기에 (기초를 공부하는 저에게) OpenGL 작업의 큰 부분을 차지하는 것은 3D 좌표를 화면에 맞게 2D 픽셀로 변환하는 작업입니다.
3D 좌표를 2D 좌표로 변환하는 작업은 OpenGL의 그래픽 파이프라인(graphics pipeline) 에 의해 관리됩니다. 그래픽 파이프라인은 여러 단계가 존재하지만 간단하게 보자면 크게 두 개의 부분으로 나뉠 수 있습니다:
- 하나는 3D 좌표를 2D 좌표로 변환하는 것이고,
- 다른 하나는 2D 좌표를 실제 색이 들어간 픽셀로 변환하는 것입니다.
3D 좌표가 2D 좌표로 변환되기 위해서는 다음과 같은 변환을 겪어야 합니다.
Object Coordinates
객체의 Local Coordinates이며 변형이 적용되기 전의 객체의 초기 위치 및 방향입니다.
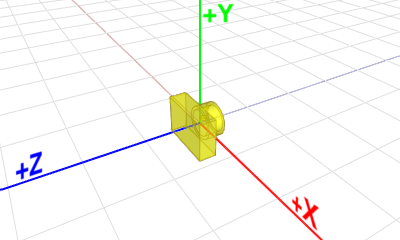
즉, 다음과 같이 모든 객체는 중심점을 (0,0,0)으로 설정한 고유의 축이 존재합니다.
World Coordinates
아래와 같이 모든 객체는 World Coordinates 안에 존재합니다.
Object Coordinates를 World Coordinates로 바꾸기 위해서는 Model Matrix을 곱하면 됩니다.
하지만, 여기서 중요한 것은 OpenGL의 World Coordinates가 Geographic World Coordinates(지리 좌표계)와 축이 다르다는 것만 알면 됩니다.
OpenGL의 World Coordinates(좌) / Geographic World Coordinates(우)
Eye Coordinates
Eye Coordinates는 카메라의 관점에서 바라보는 공간입니다. 이 공간은 원점 (0,0,0)에 고정된 카메라가 항상 -Z 축을 보는 공간입니다.
OpenGL 카메라는 항상 원점에 있고 눈 공간에서 -Z를 향합니다.
방금 전 우리는 Object Coordinates를 World Coordinates로 바꿨습니다. 여기서 View Matrix을 곱하면 World Coordinates에서 Eye Coordinates로 변환이 가능합니다.
하지만 수식을 본다고 모든 것이 이해되지 않습니다.
아래 그림을 통해 다시 생각해봅시다.
카메라가 World space의 (2,0,3)에 있고 (0,0,0)을 보고 있다고 가정합니다. 이 경우에 대한 View Matrix를 구성하려면 세계를 (-2,0,-3)으로 변환하고 Y축을 따라 약 -33.7도 회전해야 합니다. 결과적으로 가상 카메라는 원점에서 -Z 축을 향하게 됩니다.
물론 수학적 계산을 통해 직접 View Matrix를 구현할 수 있습니다. 하지만 그것이 복잡하다면 GLM에서 View Matrix를 구하기 위해 glm::lookAt 함수를 사용하면 됩니다. glm::lookAt의 파라미터로 Position과 Target 그리고 Up vector를 받습니다.
이동하는 오리 예제를 다시 생각해봅시다. glm::lookAt 인자로 현재 카메라의 위치 (2,0,3) 과 바라보고 있는 위치 (0,0,0) 그리고 Eye space에서 높이는 y축이 담당하고 있으니 Up vector로 (0,1,0) 을 입력하면 손쉽게 View Matrix를 얻을 수 있습니다.
혹시 GLM의 도움을 받지 않는다면 [여기]를 참고하여 View Matrix를 작성할 수 있습니다.
Clip Coordinates
먼저 Projection Matrix을 곱하면 Eye Coordinates에서 Clip Coordinates로 변환이 가능합니다.
Clipping이란 오려낸다는 의미입니다.
즉, OpenGL에서 Clip Coordinates란 지정된 범위의 좌표를 받아들이고 이 범위에서 벗어난 모든 좌표는 clipped(자르다)됩니다. 범위를 지정하는 것은 2가지 방법으로 나뉩니다.
Near clip plane부터 Far clip plane 사이의 공간을 절두체(Frustum)라고 부릅니다.
- Orthographic projection
orthographic projection 행렬은 원근감이 없는 정육면체와 같은 절두체 상자를 정의합니다.
orthographic 절두체는 절두체 내부에 있는 모든 좌표들을 NDC로 직접 매핑합니다. 각 벡터의 w 요소를 건드리지 않기 때문입니다. 만약 w 요소가 1.0이라면 perspective division은 좌표를 수정하지 않습니다.
orthographic projection 행렬을 생성하기 위해 GLM의 glm::ortho 함수를 사용합니다.
- Perspective projection
원근감(Perspective)은 멀고 가까운 거리에 대한 느낌. 즉, 멀리 있는 건 작게, 가까이 있는 건 크게 그리는 방법입니다.
projection 행렬은 주어진 절도체를 clip된 공간에 매핑할 뿐만 아니라 각 vertex 좌표의 w 값을 조작합니다. 시점으로부터 vertex 좌표가 멀어질수록 이 w 요소가 증가합니다. 좌표들이 clip space로 변환되고 나면 그들은 -w ~ w 범위 안에 있게 됩니다.
perspective projection 행렬을 생성하기 위해 GLM의 glm::perspective 함수를 사용합니다.
Orthographic projection과 Perspective projection 행렬을 GLM 도움 없이 계산하고 싶다면 [여기]를 추천 드립니다.
Normalized Device Coordinates
OpenGL은 각 vertext shader 실행 된 후 우리가 그리기 원하는 모든 vertex들이 정규화된 디바이스 좌표로 표시되기를 원합니다. 즉, 각 vertex의 x, y, z 좌표가 -1.0 ~ 1.0 범위 안에 있어야 합니다.
직교 투영(orthographic projection)이라면 다음과 같이 절두체 공간이 변환되어야 합니다.
원근 투영(perspective projection)이라면 다음과 같이 절두체 공간이 변환되어야 합니다.
위의 Clip Coordinates에서 Projection Matrix 연산으로 구한 (x, y, z, w)를 (x/w, y/w, z/w, 1)와 같이 w로 나누어 주면 NDC 좌표로 변환됩니다.
Window Coordinates
이 부분은 실제로 화면에 출력되는 Space를 의미합니다. 아래 그림과 같이 NDC로 정규화된 좌표를 Viewport transform을 사용하여 Window Coordinates로 변환합니다. Viewport는 Screen의 왼쪽 하단이 기준점 (0,0) 입니다.
Viewport를 정의하기 위해 x, y, width, height를 전달 받으며, x, y는 Viewport의 좌측 하단 좌표를 의미하고 width,height는 x, y로부터 넓이와 높이가 됩니다.
Window Coordinates의 좌표를 계산하고 싶으면 다음 수식을 사용하면 됩니다.
여기서 w=width, h=height, f=far, n=near 입니다.
Reference
• http://www.songho.ca/opengl/gl_transform.html
• http://www.songho.ca/opengl/gl_camera.html
• https://heinleinsgame.tistory.com/11
• http://www.codinglabs.net/article_world_view_projection_matrix.aspx
• https://glumpy.readthedocs.io/en/latest/_images/projection.png
• https://www3.ntu.edu.sg/home/ehchua/programming/opengl/cg_introduction.html
• https://gandis0713.github.io/2021/05/09/graphics-common-webgl-coordinates/

![[그림 1]](/assets/img/post/gl_pipeline.png)
![[그림 2]](/assets/img/post/gl_model.png)
![[그림 3]](/assets/img/post/gl_world.png)
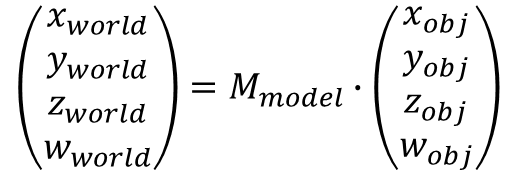
![[그림 4] OpenGL의 World Coordinates(좌) Geographic World Coordinates(우)](/assets/img/post/gl_axis.png)
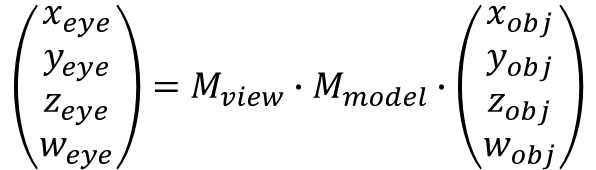
![[그림 5] Eye space로 이동하는 오리](/assets/img/post/gl_camera02.gif)
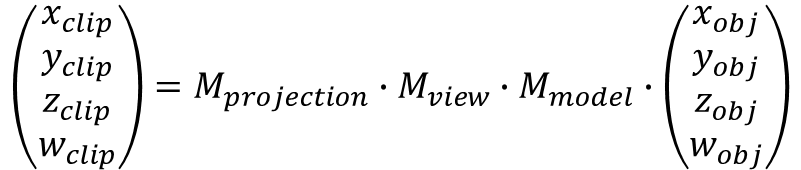
![[그림 6]](/assets/img/post/gl_clip.png)
![[그림 7]](/assets/img/post/gl_frustum.png)
![[그림 8]](/assets/img/post/gl_ortho.png)
![[그림 9]](/assets/img/post/gl_ndc.png)
![[그림 8]](/assets/img/post/gl_perspective.png)
![[그림 11]](/assets/img/post/gl_screen.png)
